an interpretation of my bko scheme

I think it is long past time to try and give an interpretation of my BKO scheme. I guess the simplest description is that it is a quite general representation for networks. Certainly static networks, but also a lot of machinery to manipulate more dynamic networks. The long term aspiration is that in its simplest form the brain is a network, albeit a very, very large and complex one, so perhaps we could use some of the BKO structures to approximate a brain? The question is though, by analogy with human flight, are we trying to build a bird with all its intricate details, or just something that flies using aerodynamic principles and simple non-flapping wings? I think with our BKO scheme we are building a plane.

Now, back to the very basics!
Recall |some text> is a ket. Sure, but what is less clear is that |some text> can be considered a node in a network. So every ket in some sw file, corresponds to a node in the network represented by that sw file. In the brain they often map to concepts. For example |hungry>, |emotion: happy>, |url: http://write-up.semantic-db.org/>, |shopping list>, |person: Mary> etc.

And it is known (from epilepsy surgery) that there are specific neurons for say "Bill Clinton" and "Halle Berry". So we can assume our brain sw file will include the kets |person: Bill Clinton> and |person: Halle Berry>.

Further, it is well known there are mirror neurons and place neurons. So for example, watching someone eat stimulates, to a lesser or greater degree, the same neuron as thinking you want to eat, or actually eating. And in rat brains there are specific neurons that correspond to places. Which implies in a brain sw file we will have corresponding kets such as |eating food>, and |cafe near my house>.

But we can also have kets that have not a lot of meaning by themselves. They only acquire meaning in a superposition with other such kets. The best example I have is for web-page superpositions. These being quite close to the SDR's of Jeff Hawkins (Sparse Distributed Representations).

But we diverge from SDR's in that superpositions are not restricted to coefficients in {0,1}. Our superpositions can have arbitrary float coefficients, though almost always positive. The interpretation being that the coefficient of a ket is the strength that ket is currently activated. I guess in the brain this probably corresponds to how rapidly a neuron is firing within some integration period. An example being: 0.8|emotion: sad> + 12|hungry> corresponds to "a little sad but very hungry".

Next, we can use this to build static networks.
For example these simple learn rules:

op1 |u> => 7.2|a> + 0.02|b> + 13|c> + |d>
op2 |v> => 5|x> + 0.9|u> + 2.712|z>

Can be interpreted to mean:

op1 links the node |u> to |a> with link strength 7.2
op1 links the node |u> to |b> with link strength 0.02
op1 links the node |u> to |c> with link strength 13
op1 links the node |u> to |d> with link strength 1

op2 links the node |v> to |x> with link strength 5
op2 links the node |v> to |u> with link strength 0.9
op2 links the node |v> to |z> with link strength 2.712

And that should be sufficient to construct arbitrary static networks. For dynamic networks we need more work. For example, currently it is impossible to associate a "propagation time" with the links. Which contrasts with the brain, where it is obvious different pathways/links take different times to travel along. Whether this feature is important in building a "plane" I don't yet know. If it is though, I can imagine a couple of ways to roughly implement it. For example, the proposed swc language, which is an extension of the current sw file format, to include more familiar programming language structures could help with this.

Now, for dynamic networks we need our suite of function operators, and stored rules, and to a lesser extent memoizing rules. "#=>" and "!=>" respectively. I suspect we can already represent a lot of dynamic networks with what we already have. And as needs arise we can add a few new function operators here and there. But for a full brain, we almost certainly need the full swc language, or the sw/BKO python back-end.

Quite bizarrely there seems to be some correspondence to our structure, intended to describe a brain, with the notation used to describe quantum mechanics. I don't know how deeply it goes, though assuming too deeply would probably be a bit crazy. There is the obvious similarity with the notation, the borrowed kets, bra's, operators and superpositions. But also wave function collapse is very close to our weighted-pick-elt operator. And making a quantum measurement is quite close to asking a question in the console.

For example:

sa: is-alive |Schrodinger's cat> !=> normalize weighted-pick-elt (0.5|yes> + 0.5|no>)

sa: is-alive |Schrodinger's cat>
|yes>

There are of course some obvious differences. The biggest being that QM is over the complex numbers, and BKO is over real valued floats. And QM has a Schrodinger equation, and plenty of other maths that is not replicated in the BKO scheme. Though of course to build a full brain we would need some kind of time evolution operator. But it is unclear what form that would take.

Finally, the idea of a path integral. That a particle in some sense travels through space-time from starting point to end point along all possible pathways is somewhat unobvious to the non-Feynman's of the world. Yet the idea that a spike train travels from starting neuron to end neuron along all possible brain pathways is obvious, and a trivial observation. This correspondence is kind of weird. And I'm not sure how superficial or deep it really is. Given this correspondence maybe it is appropriate to call a brain "brain-space"? Where concepts map to neurons, and neurons map to a 3D location in a physical brain. And operators map superpositions to superpositions, and propagate signals through brain-space.

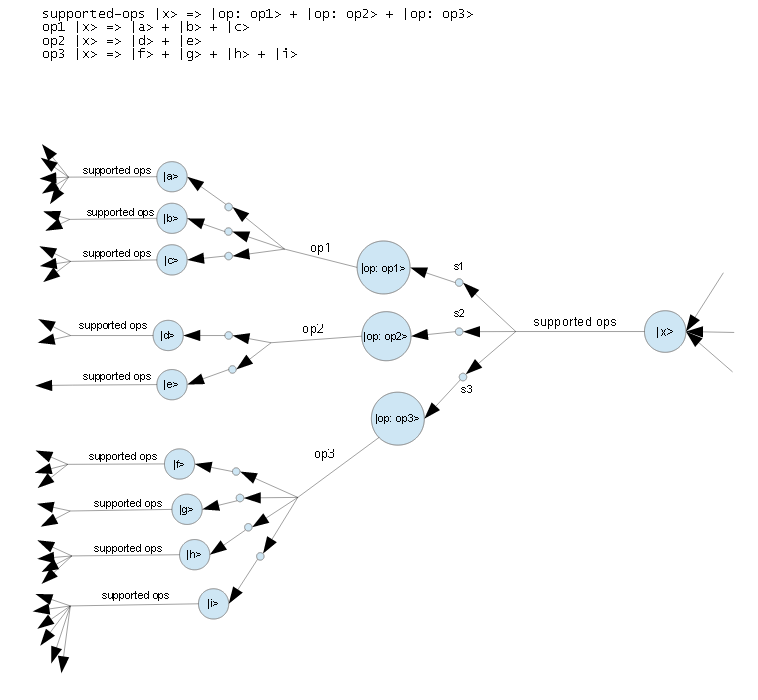
Let's finish with one possible mapping from simple BKO learn rules to a neural structure:

where:
- the BKO is:

supported-ops |x> => |op: op1> + |op: op2> + |op: op3>
op1 |x> => |a> + |b> + |c>
op2 |x> => |d> + |e>
op3 |x> => |f> + |g> + |h> + |i>

- large circles correspond to neuron cell bodies
- small circles correspond to synapses
- labeled lines correspond to axons

But this picture was from a long time ago. I now think it is probably vastly too simple!

Home
previous: new function operator inhibition
next: revisiting the letter rambler

updated: 19/12/2016
by Garry Morrison
email: garry -at- semantic-db.org